9/19 월
학습한 것들:
파이썬의 배경: 크리스마스에 뚝딱 만든 언어, 하지만 만들 때는 몰랐으나 나중에는 전 세계적으로 많이 쓰이는 언어가 되었다
개발 환경:
지금 상황으로 보면 vscode랑 miniconda 조합이 제일 좋은 것 같다. 아무래도 miniconda를 사용하면 패키지 관리도 쉬워지고 파이썬 버전도 다르게 설정할 수 있으니 좋다. vscode의 장점은 Intellicode가 내장이 되어있기 때문에 코딩이 쉬워진다. 게다가 web 버전의 jupyter notebook과 달리 vscode에서 돌리면 디버깅도 쉽게 할 수 있어서 1석 2조이다.
벡터: 차원상의 점
- 파이썬에서는 list나 np.array로 표현 가능
- 1차원일 때에는 수직선, 2차원일 때에는 좌표평면, 3차원은 공간처럼 이런 느낌으로 생각하면 된다
- 벡터는 점의 상대적인 위치를 나타내는 것이다
- 같은 크기의 백터끼리는 덧셈, 뺄셈, 그리고 성분곱 가능
벡터의 노름: 원점부터의 거리
- L1= 변화량의 절댓값의 합 (택시 기하학을 생각하자)
- np.abs 하고 np.sum
- L2 = 원점으로부터의 직선거리 (유클리드 거리)
- np.linalg.norm
벡터 사이의 거리: 벡터의 뺄셈
θ = cos-1 [ (a · b) / (|a| |b|) ]
벡터의 내적(inner product)을 이용한다
import numpy as np
v= np.inner(x,y)/(l2_norm(x)*l2_norm(y))
theta=np.arccos(v)내적은 두 벡터의 유사도를 측정하는 데 사용 가능하다
회고:
오늘부터 5개월간의 부스트 캠프 시작이다. 처음에 OT 하고 여러 가지 말들을 들으며 시작했다. 열심히 해야겠다. 아무래도 나만 우리 조에서 23학번이기 때문에 자연스럽게 동생(?), 막내 역할을 맡게 되었다. 지금은 기초를 배우니까 쉬운데 나중을 위해서 열심히 기초를 쌓아야겠다.
9/20 화
학습한 것들:
변수: 메모리 주소를 가지고 있고 값을 그 메모리에 저장해준다
파이썬은 Dynamic Typing을 사용함
2차원 리스트를 복사할 때는 copy.deepcopy를 써주자. 리스트는 메모리를 가리키기 때문에 그냥 shallow copy 하면 문제가 생긴다.
parameter: 함수의 입력 값 인터페이스
argument: 실제 Parameter에 대입된 값
%string, format 함수, fstring으로 string formatting을 할 수 있음
조건문과 반복문: for, if, while, while.. else
==는 값을 비교하지만 is는 메모리 주소를 비교한다
all()을 쓰면 안에 있는 bool이 모두 참일 때만 True를 반환한다
행렬: 2차원 배열
x=np.array([1,2,3],[4,5,6],[7,8,9]])행 벡터, 열 백터처럼 나눌 수 있음
전치 행렬(transpose matrix)은 row와 column의 index가 바뀌어 있음
행렬은 공간 안에서 여러 개의 점들이라고 생각할 수 있음
행렬도 벡터처럼 덧셈, 뺄셈, 성분곱, 스칼라곱을 할 수 있음
행렬 곱셈에서는 i번째 행 벡터와 j번째 열 백터 사이의 내적을 값으로 가지는 행렬을 계산한다
- 2x4 행렬과 4x3 행렬을 곱하면 2x3행렬이 답으로 나온다
- @을 numpy에서 사용한다
행렬 내적은 np.inner를 사용하여 i번째 행 벡터와 j번째 "행"백터 사이의 내적을 값으로 가지는 행렬을 계산한다
행렬은 벡터를 다른 차원으로 바꾸어주는 연산자라고 이해해도 된다. 행렬곱을 통하여 이 과정을 수행한다. 모든 선형 변환은 행렬곱으로 계산을 할 수 있다
역행렬은 행과 열 숫자가 같고 determinant이 0이 아닐 때만 계산할 수 있다. 역행렬과 행렬의 곱셈은 항등 행렬이다 (대각선이 1이고 나머지는 0인 행렬). np.linalg.inv
역행렬을 계산할 수 없으면 pseudo-inverse 또는 Moore-Penrose 역행렬을 이용한다. np.linalg.pinv를 사용하여 유사 역행렬을 계산할 수 있다.
유사 역행렬을 이용하여 선형 회귀식과 연립방정식의 해를 찾을 수 있다
미분: 변화율을 측정하기 위한 도구 f'(x)
- 함수 f의 (x, f(x)) 좌표에 있는 점에서의 접선의 기울기
파이썬에서도 sym.diff로 미분을 컴퓨터로 계산 가능
접선의 기울기를 알면 어디로 움직여야 함숫값이 증가 또는 감소하는지 알 수 있다
미분 값을 더하면 경사 상승법(극대 값 구하기)
미분 값을 빼면 경사 하강법(극소값 구하기)
극값에 도착하면 기울기가 0이므로 움직이지 않는다
만약에 벡터를 입력으로 경사 하강을 하면 편미분을 사용한다
- 각 "변수별로 편미분"을 계산한 gradient vector을 이용해서 경사 하강이나 경사 상승법에 사용 가능
gradient_w = np.sum((_y - train_y) * train_x) / n_data
gradient_b = np.sum((_y - train_y)) / n_data- 그래서 변수별로 편미분을 계산하였을 때 w는 chain-rule 때문에 train_x를 곱해줘야 하지만 b는 편미분 하면 x가 사라지기 때문에 할 필요가 없다

- slope field 같은 느낌
- -∇f 가 gradient vector
회고:
오늘은 어려운 개념들을 많이 배웠다 역시 인공지능은 수학인가 보다. 프레젠테이션을 만들면서 재미있었다. 내일은 심화 문제들을 다 풀어야겠다. 왜 변수별로 편미분 하고 왜 식이 그렇게 나오는지 알게 되어서 흥미로웠던 것 같다.
9/21 수
학습한 것들:
Stochastic Gradient Descent(SGD): 데이터 일부를 활용하여 업데이트
볼록이 아닌 목적식을 SGD를 통해 최적화 가능
랜덤 성 덕분에 딥러닝에서는 더 좋은 결과를 보여줌
목적식을 근사하기 때문에 같은 결과가 나오지 않을 수 있지만 극소점에서 최소점으로 갈 수 있게 탈출할 수 있다
데이터를 나누어서 로드하기 때문에 데이터 크기가 클 때 SGD를 쓰면 하드웨어에 무리가 가지 않는다
컴퓨터는 문자를 숫자로 저장해서 받는다(bit 단위로)
파이썬은 call by object reference 방식을 차용하기 때문에 객체가 아닐 경우에는 값을 복사해서 함수로 넘기고 맞다면 메모리 주소를 인자로 넘긴다
전역 변수는 함수에서 사용 가능하지만 같은 이름의 변수를 사용하면 지역변수가 생김
type 힌트를 통해서 버그를 방지할 수 있다
세 개의 따옴표로 함수의 대한 사전 스펙을 함수 밑에 적을 수 있다
zip: 두 개의 리스트를 병렬적으로 추출할 수 있음
lambda: 익명 함수, 함수를 선언하지 않고도 만들 수 있음.
reduce: 리스트에 똑같은 함수를 적용해서 통합
lambda나 reduce는 직관성이 떨어져서 사용을 권장하지 않음
iterable object들은 __next__와 __iter__이 있기 때문에 iter()과 next()로 하나씩 불러올 수 있음
generator: 원소가 사용되는 시점에 값을 반환
- 메모리에 무리가 가지 않음
- yield를 사용함으로써 필요할 때만 불러올 수 있음
회고:
오늘은 멘토 분과 만나서 멘토링 시간을 가졌다. 오늘은 다양한 심화 과제들도 풀어봤는데 아무래도 수학이 중요하다는 것을 느꼈다. 이제부터는 논문도 읽고 공부를 더 해봐야겠다.
9/22 목
학습한 것들:
keyword arguments: 자기가 원하는 인자를 원하는 순서대로 넣을 때
default arguments: 입력하지 않아도 기본 값이 설정되어 있음
variable length asterisk: *arg를 보통 사용, parameter 이후의 값을 tuple로 저장함
keyword variable length: **kwargs 보통 사용, dict형식으로 변수와 값을 저장함
asterisk를 사용하게 되면 tuple, dict 같은 자료형을 unpacking 해서 넘겨줌
percenptron들의 사이의 화살표는 W매트릭스이다
softmax: 출력을 확률로 변환시켜주는 활성 함수
- 분류 문제를 풀 때 유용하다
- np.max를 벡터에서 빼줌으로써 overflow를 방지한다
- 추론 단계에서는 그냥 one-hot 벡터를 사용해서 최댓값만 1을 가지는 백터를 출력한다

신경망은 선형 모델과 활성 함수를 합성한 함수이다
- 활성 함수로 선형 모델을 비선형으로 변환할 수 있다
- ReLU, tanh, sigmoid 등의 활성 함수를 사용하지만 딥러닝에서는 보통 ReLU를 사용한다
- 다층 신경망: 딥러닝의 다른 이름
활성화 함수는 각 perceptron에 각각 적용된다
forward propagation: 순차적으로 신경망 계산
층을 여러 개 쌓는 이유는 목적함수를 근사하는데 필요한 뉴런의 숫자가 빨리 줄기 때문에 더 효율적이다. 하지만 최적화가 더 힘들어질 수도 있다
backpropagation: 각 층의 사용된 parameter(w, b)를 학습한다
- chain rule을 이용하여 gradient vector를 전달한다 (자동 미분)
딥러닝은 확률론 기반의 기계학습 이론에 바탕을 두고 있음
손실 함수들의 특성을 이용해서 학습을 유도할 수 있음
이산형(discrete) 확률변수: 경우의 수를 모두 고려해서 더해서 모델링
연속형(continuous) 확률변수: 확률변수의 밀도를 고려해서 적분을 통해 모델링
결합 분포는 확률분포의 형태와 관계가 없다(discrete이어도 continous로 바뀔 수 있음)
조건부 확률분포: P(x|y) 어떤 조건 y일 때의 x일 확률
- 분류 문제에서 사용
조건부 기댓값: E(x|y) 적분을 사용한다
- 회귀 문제에서 사용
기댓값: 데이터를 대표하는 통계량
- 연속: 적분
- 이산: 급수
Monte Carlo 샘플링 방법: 데이터를 이용해서 기댓값을 계산하는 방법
통계적 모델링은 적절한 가정 위에서 확률분포를 추정하는 것이 목표고, 유한한 데이터로 정확하게 분포를 알아낼 수가 없기 때문에 근사적으로 추정할 수밖에 없다
모수적(parametric) 방법론: 특정 확률분포를 따른다 가정하고 parameter 찾기
비모수적(nonparametric) 방법론: 데이터의 따라 모델의 구조 및 모수의 개수가 유연하게 바뀔 때, 기계학습이 보통 여기에 해당됨
베르누이 분포: 0과 1만 가짐
카테고리 분포: 이산적인 값을 가짐
베타 분포: 0과 1 사이에서 값을 가짐
감마 분포, 로그 정규분포: 0 이상의 값을 가짐
정규분포, 라플라스 분포: R전체의 값을 가짐
정규분포의 모스는 평균과 분산이라는 통계량으로 추정할 수 있다
표본 분산에서 n-1로 나누는 이유는 표본 분산은 분산을 과소평과 하게 되어서 이를 보정해주려면 표본 분산의 분모를 작게 만들어준다
표집 분포: 통계량의 확률분포
중심 극한 정리(Central Limit Theorem): n이 커질수록 평균의 표본 분포가 정규분포에 근사한다 (모집단의 분포가 정규분포를 따르지 않아도 성립한다)
최대 가능도 추정법(Maximum Likelihood Estimation, MLE): 가장 가능성이 높은 모수를 추정하는 방법
회고:
7강 통계학 맛보기를 하나도 이해를 못 했다. ㅠㅠㅠㅠ 아무래도 나중에 천천히 기초부터 배워야 할 것 같다.
9/23 금
학습한 것들:
조건부 확률: a가 일어난 상황에서 b가 일어날 확률 P(B|A)

베이즈 정리: 조건부 확률을 이용해서 정보를 갱신하는 법

사후 확률: 데이터를 관찰했을 때 이 parameter이 성립할 확률
사전 확률: 데이터가 주어지기 전에 parameter이 성립할 확률
가능도: 현재 주어진 모수에서 이 데이터가 관찰될 확률
Evidence: 데이터 자체의 분포

베이즈 정리를 통해서 새로운 데이터가 들어왔을 때 이미 계산한 사후 확률을 사전 확률로 사용하여 갱신된 사후 확률을 계산할 수 있음
조건부 확률을 인과관계를 추론하는데 함부로 쓰면 안 됨, 중첩 요인을 제거하자
convolution연산은 kernel을 입력 벡터 상에서 움직이면서 계산
- 신호를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 필터링할 수 있음
- 다양한 차원에서 계산 가능함
- 데이터의 성격에 따라 사용하는 커널이 달라짐

채널이 여러 개인 2차원 입력의 경우 2d conv를 채널 개수만큼 적용한다
convoultion연산의 미분은 convolution이다
시퀀스 데이터를 다룰 때에는 순서를 바꾸지 않게 조심해야 한다
- 과거의 모든 정보들이 중요한 것은 아니다
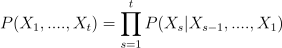
시퀀스 데이터는 가변적이기 때문에 이에 적용할 수 있는 모델이 필요함

RNN의 역전 파는 BPTT(BackPropagation Through Time)를 사용
BPTT는 시간이 길어질 수롤 기울기가 소실되기 때문에 길이를 끊어주는 게 중요하다. 이를 위해 LSTM과 GRU가 개발되었다
회고:
오늘 강의를 다 들었다. 어려운 수학 개념들이 많았지만, 그래도 잘 설명해주셔서 어떻게 잘 들은 것 같다. 주말에는 심화 과제와 복습을 해봐야 할 것 같다.
'잡다한 것들 > 부스트캠프 AI Tech 4기' 카테고리의 다른 글
| 6주차 학습 일지 - CV 기초대회 (0) | 2022.10.24 |
|---|---|
| 부스트캠프 5주차 학습 일지 - Computer Vision Basics (0) | 2022.10.18 |
| 부스트캠프 4주차 학습 일지 - Computer Vision Basics (0) | 2022.10.11 |
| 부스트캠프 3주차 학습 일지 - Deep Learning Basics (0) | 2022.10.03 |
| 부스트캠프 2주차 학습 일지 - Pytorch Basics (0) | 2022.09.26 |


