오늘은 IOI 2001년도 Day 2에 나온 Double Crypt라는 백준에 24218번, 24219~24221번, 24222~24228번으로 올라온 문제를 풀어보려 한다. 10개의 문제를 3구간으로 나눈 이유는 이 구간들을 기점으로 난이도가 바뀌기 때문이다.
문제 설명
이 문제에서는 AES라는 암호화 알고리즘이 있는데 https://www.crocus.co.kr/1230에 있는 블로그에 있으니 구조 설명은 그곳을 참고하도록 하자. 일단 중요한 것은 암호학이 아니라 그 암호화할 때 쓰는 key 값을 어떻게 구할 것인가 이다. 당연히 생각해보면 이건 보안을 위한 알고리즘인데 이게 우리가 뚫을 수 있다면 그건 좋은 알고리즘이 아니다.
다행히, 문제에서는 key값은 앞에 최대 hex 5자리(hex 하나 당 4비트)와 나머지는 0으로 구성되어 있다고 한다. 구해야 할 hex자릿수와 처음에 들어간 32자리 hex 문자열과 AES 암호화를 두 번을 거치고 나온 32자리 hex 문자열 두 개가 입력으로 주어졌을 때, 우리의 일은 2개의 키값을 찾는 것이다. 그리고, 이 문제에는 프로그램을 제출하는 게 아니라 이미 주어진 입력 문자열 2개를 보고 답을 출력하기만 하면 되기 때문에 외부 라이브러리를 사용해서 precomputation(전처리) 해주면 된다.

24218번
이 문제는 문제가 헷갈려서 20분 동안 고생했던 문제다. 진짜로 프로그램을 짜는 건 24219번 부터이고 이 문제는 그냥 예제 출력에 있는 답을 출력해주면 된다. double_1.in 파일을 확인해보면 예제 입력과 똑같은걸 볼 수 있다

24219~24221번
이때부터 코딩이 필요한 시간이다. 이 게시물을 참고해서 풀어 보았다. https://www.acmicpc.net/board/view/82320 이 게시물이 없었다면 감도 잡지 못했을 것 같아서 감사하다.
글 읽기 - encrypt / decrypt 함수 예제
댓글을 작성하려면 로그인해야 합니다.
www.acmicpc.net
코드
from Crypto.Cipher import AES
from itertools import product
def encrypt(ptext: str, key: str) -> str:
ptext, key = bytes.fromhex(ptext), bytes.fromhex(key)
ctext = AES.new(key, AES.MODE_ECB).encrypt(ptext)
return ctext.hex().upper()
s=int(input())
text=input()
text_encrypted=input()
hex_values=["0","1","2","3","4","5","6","7","8","9","A","B","C","D","E","F"]
possible_keys=product(hex_values,repeat=s*2)
for k in possible_keys:
key1="".join(k[:s])+"0"*(32-s)
key2="".join(k[s:])+"0"*(32-s)
encrypted_outcome=encrypt(encrypt(text, key1),key2)
if encrypted_outcome==text_encrypted:
print(key1)
print(key2)
break설명
일단은 밑에 있는 명령어를 터미널에 입력해서 pycrypto나 PyCryptodome을 받아준다. 이 라이브러리는 파이썬에서 암호화에 관련된 작업들을 가능하게 만들어준다.
pip install pycryptoAES모듈을 import 시켜주면 모든 준비가 되었다.
from Crypto.Cipher import AESAES 모듈에서 AES.new(key, mode=AES.MODE_ECB)를 사용하면 새로운 cipher object를 만들 수 있다. 여기서 encrypt(인풋)을 한다면 이 key로 설정돼있는 cipher object가 그 입력을 AES 암호화시켜준다. 마찬가지로 decrypt를 한다면 복호화를 시켜준다. 여기서 MODE_ECB는 electronic codebook의 줄임말인데, 16개의 byte로 이루어진 블록으로 암호화하는 메시지를 나눠서 따로따로 encrypt를 수행한다.

여기서 우리에게 입력으로 주어진 hex는 자리다 4bit이고, encrypt는 16개의 byte가 하나의 블록이다. 우리는 32개의 hex digit이 있기 때문에 계산해보면 16개의 byte가 딱 맞게 나온다는 것을 알 수 있다(byte는 2개의 hex로 이). 저기서 모듈에 나와있지 않고 직접 구현한 encrypt는 이 hex로 되어있는 문자열을 byte로 바꾼 뒤 cipher object에 encrypt를 하고 나온 값을 다시 hex로 돌려주는 함수이다.
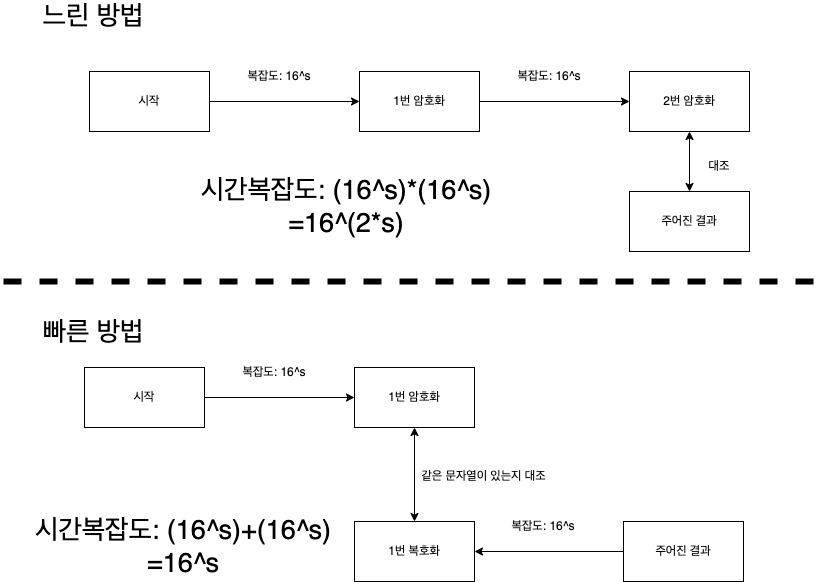
자, 이제 생각해보자. 키값의 크기는 AES-128을 사용하기 때문에 32자리이다. 그리고 맨 처음 줄에 나오는 숫자의 정체는 키의 왼쪽부터 4*s비트 즉, s 만큼의 16진법 자리는 의미가 있지만, 나머지 32-s 자리는 모두 0이다라고 말한다. 그렇다면 s=1일 때는 key당 맨 처음 한자리만 맞추면 되기 때문에 key당 16번만 해보고 결과를 맞추어보면 된다. 여기는 double crypto 즉 두 번의 AES 암호화를 거치기 때문에 두 개다 맞춘다면 16*16=256번만 연산해보면 된다. s=2일 때는 (16^2)*(16^2)=65536번 정도면 풀리기 때문에 모든 key 조합을 찾아서 encrypt 해본 후, 그 encrypted 한 게 3번째 줄에 있는 결과와 같으면 두 개의 key를 출력해서 이 key를 제출하면 정답을 받을 수가 있다.
from itertools import product을 해주면 product(*iterables, repeat=1) 을해서 repeat만큼의 중복해서 iterable에 있는 모든 중복되는 원소의 조합을 받을 수가 있다. 우리는 2개의 키를 위한 key값을 받아야 하니 hex value에서 s의 2배만큼 중복이 있을 수 있는 조합을 만들면 된다.
hex_values=["0","1","2","3","4","5","6","7","8","9","A","B","C","D","E","F"]
possible_keys=product(hex_values,repeat=s*2)
이제부터 for loop으로 가능한 key값들을 돌면서 뒤에는 32-s 만큼에 0을 붙여서 key1, key2로 2번째 줄에 있는 처음 암호화할 text를 encrypt 해준다. 만약에 이 key값들 2개가 마지막 줄에 있는 결과와 같다면 그 key값을 반환해주면 된다. "". join(k [:s]) 이랑 "". join(k [s:])을 해줌으로써 아까 전에 2*s만큼 받아놓은 조합을 반으로 쪼갠다.
for k in possible_keys:
key1="".join(k[:s])+"0"*(32-s)
key2="".join(k[s:])+"0"*(32-s)
encrypted_outcome=encrypt(encrypt(text, key1),key2)
if encrypted_outcome==text_encrypted:
print(key1)
print(key2)
여기까지 한다면 double crypt 2부터 4까지는 풀 수 있다. 근데 이제 s가 하나씩 늘 때마다 이 브루트 포스 방식을 사용하면 256배씩 복잡도가 늘어나기 때문에 s=5일 때에는 16^10=1099511627776가지의 조합이 가능하다. 이건 상당히 느리기 때문에 새로운 방식을 double crypt 5부터 적용해야 한다.
24222~24227번
여기서도 https://www.acmicpc.net/board/view/82730에 있는 게시물에서 힌트를 얻어서 풀어봤다.
코드
from Crypto.Cipher import AES
from itertools import product
def encrypt(ptext: str, key: str) -> str:
ptext, key = bytes.fromhex(ptext), bytes.fromhex(key)
ctext = AES.new(key, AES.MODE_ECB).encrypt(ptext)
return ctext.hex().upper()
def decrypt(ptext: str, key: str) -> str:
ptext, key = bytes.fromhex(ptext), bytes.fromhex(key)
ctext = AES.new(key, AES.MODE_ECB).decrypt(ptext)
return ctext.hex().upper()
s=int(input())
text=input()
text_encrypted=input()
hex_values=["0","1","2","3","4","5","6","7","8","9","A","B","C","D","E","F"]
poss_keys=product(hex_values,repeat=s)
encrypted_once=dict()
for k in poss_keys:
key1="".join(k)+"0"*(32-s)
encrypted_once[encrypt(text,key1)]=key1
poss_keys=product(hex_values,repeat=s)
for k in poss_keys:
key2="".join(k)+"0"*(32-s)
decrypted_once=decrypt(text_encrypted,key2)
if decrypted_once in encrypted_once:
print(encrypted_once[decrypted_once])
print(key2)
break
설명
여기서 대체적으로 그전에 푸는 방식과 비슷하다. 달라진 점이 있다면 이제는 16^(2*s)의 시간 복잡도로는 풀 수가 없다는 것이다. 여기서 중요한 아이디어가 있다. 이전의 풀이 방식은 시작 문자열을 2개의 key로 암호화하여 대치하여서 풀었다면, 이번에는 시작 문자열에 한 번만 암호화해주고 이미 두 번 암호화되어있는 문자열을 다른 key로 복호화해주어서 두 개가 같아지는 key1, key2 짝이 정답이다는 것을 알 수 있다. 이렇게 하면 16^(2*s)였던 복잡도가 16^s로 바뀌었다. (사실 이것도 이 암호체계는 32자리라 엄청나게 크지만 s=5라는 제한을 가진 문제를 풀기에는 충분하다)
for k in poss_keys:
key1="".join(k)+"0"*(32-s)
encrypted_once[encrypt(text,key1)]=key1
decrypt라는 encrypt와 똑같지만 encrypt(ptext)에서 decrypt(ptext)로 바꾼 함수를 정의해준 다음 encrypted_once라는 dict에 모든 한번 암호화된 결과를 dictionary에 key값으로(이 key는 암호화의 key가 아니다), value에는 첫 번째 key 값을 저장해준다. 여기서 dicitonary를 사용하는 이유는 key2로 복호화된 값이 dictionary에 존재하는지 확인하는 시간이 O(1)이기 때문에 복호화 해준 값이 이미 있는지 찾는다고 찾을 때마다 O(n)을 해줄 필요가 없어진다 (list를 저장에 사용 시).
poss_keys=product(hex_values,repeat=s)
for k in poss_keys:
key2="".join(k)+"0"*(32-s)
decrypted_once=decrypt(text_encrypted,key2)
if decrypted_once in encrypted_once:
print(encrypted_once[decrypted_once])
print(key2)
breakproduct는 iterable이기 때문에 다시 생성해주고, 이번에는 복호화를 key2로 시켜준다. 만약에 이 복호화된 값이 encrypted_once에 key(dict의 key)로 존재한다면 그것의 value와 key2를 출력해주면 된다.
후기:
암호학의 영역에 대충 발(?)만 담가본 것 같았고 암호해독이 재미있었다. 우리의 데이터가 어떻게 암호화되어 있고 얼마나 안전한지 알 수 있는 시간이었다. 나중에 암호학 관련 공부를 더 해보고 싶다.
소스코드가 있는 링크:
https://github.com/LimePencil/baekjoonProblems/tree/main/com/LimePencil
GitHub - LimePencil/baekjoonProblems: 백준 코딩문제 자바&파이썬 해답
백준 코딩문제 자바&파이썬 해답 . Contribute to LimePencil/baekjoonProblems development by creating an account on GitHub.
github.com
'PS & Algorithm' 카테고리의 다른 글
| [백준] 1437번: 수 분해 풀이 (수학적 증명 포함) (4) | 2022.09.30 |
|---|---|
| [백준] 3602번: iChess 파이썬 풀이 (0) | 2022.04.24 |
| [백준] 24954, 24955, 24956번: 쇼미더코드 2022년 1회차 파이썬 풀이 (1) | 2022.04.22 |
| [백준] 1182번, 1208번: 부분수열의 합 1,2 파이썬 풀이 (0) | 2022.04.16 |
| [백준] 1520번: 내리막 길 파이썬 풀이 (bottom-up, 비재귀) (0) | 2022.03.29 |
![[백준] 24218번, 24219~24221번, 24222~24228번: Double Crypt 파이썬 풀이](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FvctQU%2FbtrzvwSufts%2FrvHHkkYjYWk8f3ZCNNgQD1%2Fimg.png)
