[논문 리뷰] Noisy Networks for Exploration (NoisyNet)

[1706.10295] Noisy Networks for Exploration (arxiv.org)

Noisy Networks for Exploration

 

이번 논문에는 DQN에 있는 fully connected layer에 parametric 한 noise를 넣어서 유도된 stochasticity가 agent의 성능을 올려준다는 연구를 한 논문이다. 지금까지 여러 가지 DQN의 변형을 다뤘는데 아마 이 글이 Rainbow DQN전의 마지막 글이지 않을까 싶다. DQN에 관한 논문 리뷰는 아래 글을 참조하자.

 

[논문 리뷰] Playing Atari with Deep Reinforcement Learning (DQN) — LimePencil's Log (tistory.com)

[논문 리뷰] Playing Atari with Deep Reinforcement Learning (DQN)

 

 

Introduction

Optimism in the face of uncertainty이나 intrinsic motivation 같은 common heuristic reinforcement learning method 같은 경우에는 generalization과 exploration을 다른 방법을 사용한다는 것이다. Intrinsic reward 같은 경우를 예로 들면 metric을 사람이 결정하기 때문에 optimal 하다고 보기는 어렵다. 제일 좋은 방법은 exploration in the policy itself이나, 이 방법은 환경과 긴 interaction이 필요하다(not data-efficient and require simulator).

 

이 논문에서는 다른 대안을 제안하는데, 이는 바로 네트워크의 weight 자체에다가 perturbation을 주어서 exploration을 하게 만드는 방법이다. 이 perturbation은 noise distribution에서 sampling이 되고 이 variance hyperparameter 자체를 손실함수를 통해 학습을 하게 시키는 방법이다. 즉, 네트워크가 스스로 noise의 level 크기를 결정하는 방식이다. 이 방식이 computationally expensive 하다고 볼 수 있으나 사실 affine transformation이기 때문에 큰 영향은 없다.

 

또한 NoisyNet은 다른 DQN의 변형인 알고리즘 (Dueling, Double 등등)에 쉽게 implement 시킬 수 있다.

 

 

NoisyNet for Reinforcement Learning

NoisyNet이란 네트워크의 weight이나 biases를 parametric function으로 만든 noise를 입히는 것인데, 이 파라미터는 경사하강법으로 최적의 값을 찾을 수 있다. noisy parameter $\theta$를 다음과 같이 정의하는데 $$ \theta \stackrel {\text {def}}{=} \mu + \sigma \odot \epsilon$$ 여기서 $\mu, \Sigma$은 학습 가능한 파라미터이고, $\epsilon$은 평균이 0인 노이즈 벡터이다.

 

평소의 neural network의 linear layer을 다음과 같이 표현한다면 $$y = wx +b$$ noisy linear layer은 $$y \stackrel {\text {def}}{=} (\mu^w + \sigma^w \odot \epsilon^w) x + \mu^b + \sigma^b \odot \epsilon^b$$ 으로 표현할 수 있다.

 

Noise Distribution의 종류:

1. Independent Gaussian noise: noise per output
   1. Initialization: uniform distribution of $ \mu_{i,j} = \textit{U} \left[ - \sqrt{\frac{3}{p}}, \sqrt{\frac{3}{p}} \right]$ 이고 ($p$는 input의 크기), $\sigma_{i,j} = 0.017$
2. Factorized Gaussian noise: noise per input
   1. Initialization: uniform distribution of $\mu_{i,j} = \textit{U} \left[ - \frac{1}{\sqrt{p}}, \frac{1}{\sqrt{p}} \right]$ 이고 ($p$는 input의 크기), $\sigma_{i,j} = \frac{\sigma_0}{\sqrt{p}} | \sigma_0=0.5$

weight와 biase의 개수 차이를 보자  :  https://towardsdatascience.com/whats-the-role-of-weights-and-bias-in-a-neural-network-4cf7e9888a0f

 

Factorized Gaussian noise를 쓰는 이유는 random number을 generate 하는 compute시간을 줄이기 위해서 그렇다. $p$를 input, $q$를 output으로 정의한다면 Independent Gaussian noise는 $pq + q$의 noise variable을 가지고 있고 Factorised Gaussian noise는 $p+q$의 noise variable을 가지고 있다. Independent Gaussian noise는 곱셈을 가지고 있기 때문에 $p$와 $q$가 커지면 더 많은 계산이 필요하다. Factorized Gaussian noise는 $p$와 $q$가 덧셈 관계이기 때문에 수가 그렇게 빨리 커지지는 않는다. Factorized Gaussian noise가 작은 이유는 Independent Gaussian noise처럼 모든 weight에 대한 random noise를 만드는 게 아니라 input과 output의 수만큼 random noise를 만들고 weight는 이 두 값을 곱한 것으로 사용하기 때문이다.

 

 

Noise는 RL에서 중요한 exploration을 담당하게 되는데, 이를 통해 어떠한 stochasticity를 부여한다. NoisyNet에서는 자동으로 이 노이즈의 정도를 NoisyNet에서 조절하게 된다. 즉, 주입되는 noise의 정도를 agent가 자동적으로 맞춘다는 것이다.

 

DQN과 Dueling DQN에는 epsilon-greedy 방식을 쓰지 않고 NoisyNet으로 대체한다. 위에서 설명한 Factorized Gaussian Noise를 사용하고 noise sample은 각 action 전에 항상 다시 샘플 된다. DQN에서 target network와 online network의 noise를 각각 따로 생성하여 어떠한 correlation이 생기는 것을 막는다. 또한, action을 고를 때에도 다른 노이즈 샘플을 사용하고 greedy 하게 action을 선택한다. Dueling 같은 경우에도 DQN과 비슷하게 구성한다.

 

A3C 같은 경우에는 policy network의 entropy bonus를 없애고 fully connected layer을 NoisyNet으로 대체한다. A3C는 DQN과 다르게 Independent Gaussian noise를 사용한다. Entropy loss를 사용하는 이유가 deterministic 하게 하는 것을 방지하기 위해서인데, 이를 NoisyNet으로 해결했기 때문에 필요가 없어졌다. N-step return을 사용하기 때문에 n step마다 noise parameter가 새로 sampling 된다.

 

Results

https://arxiv.org/pdf/1706.10295.pdf

 

성능은 그전의 논문들과 같이 57개의 Atari게임으로 비교하였다. 비교 대상은 DQUN, Dueling DQN, 그리고 A3C이다. 점수는 그 전 논문과 같게 human normalized score로 계산되었다. 

https://arxiv.org/pdf/1706.10295.pdf

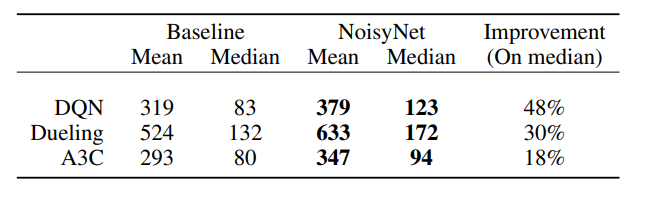
위에 있는 표와 그래프를 보면 NoisyNet이 전반적으로 성능 향상에 기여를 했다는 것을 볼 수 있다. 또한 $\sigma^w$를 학습동안 계속 추적해 봤을 때에 0으로 수렴하여 deterministic solution으로 바뀌지 않았고 증가하는 게임도 있었다. 이는 NoisyNet이 problem-specific exploration strategy를 만들었다는 모습이다.

 

Conclusion

이 논문에서는 NoisyNet이라는 새로운 탐색 기법을 소개하고 있고, 성능이 올라간 것은 optimization효과 일수도 있지만 이는 exploration과 optimization을 따로 보는 후속 연구가 필요하다. NoisyNet의 다른 장점은 noise의 정도를 RL algorithm이 결정한다는 것인데, 이는 hyperparamenter tuning의 필요를 줄여준다. NoisyNet은 다양한 FC layer이 있는 RL algorithm에 적용을 할 수 있는 좋은 기법이다.